الباب الأول

النظرية النسبية الخاصة

وضع ألبرت آينشتاين عام 1905 نظريتة الشهيرة للنسبية الخاصة والتي كان لها أعظم الأثر في الدراسات الفيزيائية. وقد جاءت هذه النظرية تتويجا لبحوث الفيزياء في القرن التاسع عشر، وخاصة ما توصل إليه ماكسويل من أن جميع الظواهر الكهربية والمغناطيسية تجمعها نظرية كهرومغناطيسية واحدة تدعو لوجود موجات كهرومغناطيسية تسير بسرعة الضوء. تقوم نظرية آينشتاين للنسبية الخاصة على فرضين أساسيين هما:

1. تكون قوانين الظواهر الفيزيائية واحدة في جميع الأنظمة القصورية وتأخذ نفس الصورة الرياضية، فمثلا يمكن التعبير عن قوانين نيوتن للحركة بنفس الشكل في جميع الأنظمة بغض النظر عن اختلاف القيم.

2. سرعة الضوء في الفراغ ثابتة دائما وقيمتها _3x10⁸m/s بغض النظر عن سرعة المصدر الضوئي نفسه أو سرعة الراصد.

نتيجة للفرض الأول نجد أنه لا يمكن قياس السرعات المطلقة وإنما تتحدد فقط السرعات بالنسبة لجسم آخر. فإذا تكلمنا عن سرعة سيارة فإنها تكون بالنسبة للأرض أما إذا وجدت سيارة أخرى تسير بنفس سرعة السيارة الأولى وفى نفس اتجاهها فإن السرعة التي يراها شخص في السيارة الثانية تكون صفرا وهكذا بالنسبة لشخص في السيارة الأولى فإنه سوف يرى السيارة الثانية تتحرك بسرعة تساوى صفر. وكنتيجة لفروض آينشتاين يمكننا بواسطة المنطق إثبات أن سرعة الضوء هي الحد الأعلى للسرعات جميعها وأنه لا يمكن لأي جسيم يحمل طاقة أن يعجل لسرعة الضوء.

ولدراسة النظرية النسبية يجب أولا دراسة قوانين التحويل بين النظم القصورية المختلفة وأهم هذه التحويلات هي تحويلات جاليليو وتحويلات لورنتز.

1. تحويلات جاليليو

        في الحركة النسبية تعتمد قيم السرعة والعجلة لأي نقطة مادية على محاور الإسناد التي تعتمد فيها هذه القيم. نفرض أن راصدين يتحركان بالنسبة لبعضهما ويرصدان في نفس الوقت جسما متحرك، نجد أنهما يصفان الجسم نفسه متحركا بسرعات مختلفة ومسارات مختلفة. ولكن يمكن أن تتفق الوصفتان إذا أجريت تحويلات في معادلة أحد الراصدين بحيث تأخذ في الاعتبار الحركة النسبية للراصدين. وتعرف هذه بالتحويلات الجاليلية نسبة إلي جاليليو أول من حل تحولات الحركة من نظام قصوري إلي نظام قصوري آخر.

        أهم فرض في التحويلات الجاليلية هو ثبات المسافة والزمن بالنسبة للراصدين في النظامين القصوريين. ونعبر عن ذلك رياضيا باعتبار محاور إحداثيات ، _X,Y,Z,t ، x’,y’,z’,t’ يعرفان النظامين المتحركان معا في الاتجاه الموجب للمحور السيني بسرعة نسبية . ونفرض أن نقطتي الأصل _O ، _O’ كانتا منطبقتين عند الزمن _t=0

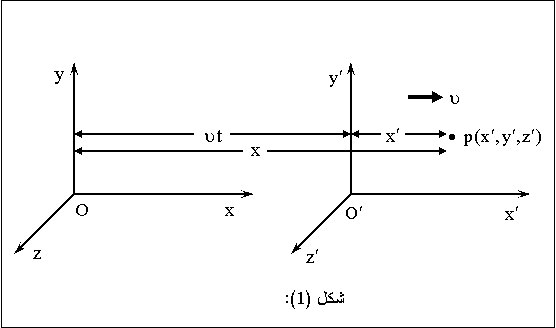
بعد فترة زمنية t ترتبط إحداثيات نقطة مثل p بالنسبة للنظام الأول بإحداثيات نفس النقطة بالنسبة للنظام الثاني بالمعادلات

                                                        (1)

ونعبر عن انطباق الزمن في المجموعتين بالمعادلة

 (2)

تسمى هذه المعادلات بالتحويلات الجاليلية وتنبني كل فروضها على أساس قوانين نيوتن، وعلى ذلك فهي صحيحة فقط طالما اعتمدت صحة هذه القوانين وذلك في حالة السرعات الصغيرة بالنسبة لسرعة الضوء.

2. تحويلات السرعة والتسارع جاليليو

        يمكن الحصول على تحويلات السرعة والتسارع بمفاضلة تحويلات جاليليو كما يأتي:

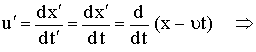
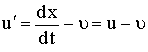                                                       (3)

حيث  السرعة في الإحداثيات المتحركة، u هي السرعة في الإحداثيات الثابتة،  هي السرعة النسبية بين الإحداثيتين.

وبالنسبة للعجلة فإننا نفاضل المعادلة (3) فنحصل على

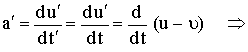
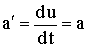                                                       (4)

حيث  هي العجلة في الإحداثيات المتحركة، a العجلة في الإحداثيات الثابتة وذلك باعتبار أن السرعة  هي سرعة ثابتة. وبالنظر إلى المعادلة (3) نجد أنه هناك تناقض مع الفرض الثاني للنظرية النسبية إذا ما سارت الإحداثيات أو النظام المتحرك بسرعة الضوء. فإذا وضعنا سرعة الضوء في الإحداثيات المتحركة

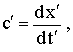
ووضعنا سرعة الضوء في الإحداثيات الثابتة

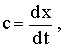
فإنه من الواضح تبعا للمعادلة (3) أن

أي أن سرعة الضوء تكون متغيرة وهذا تناقض واضح مع الفرض الثاني لآينشتاين. لذا كان لابد من وضع نظام آخر من التحويلات يفي بالغرض ولا يتعارض مع فروض النظرية النسبية الخاصة وهذا ما قام به العالم لورنتز.

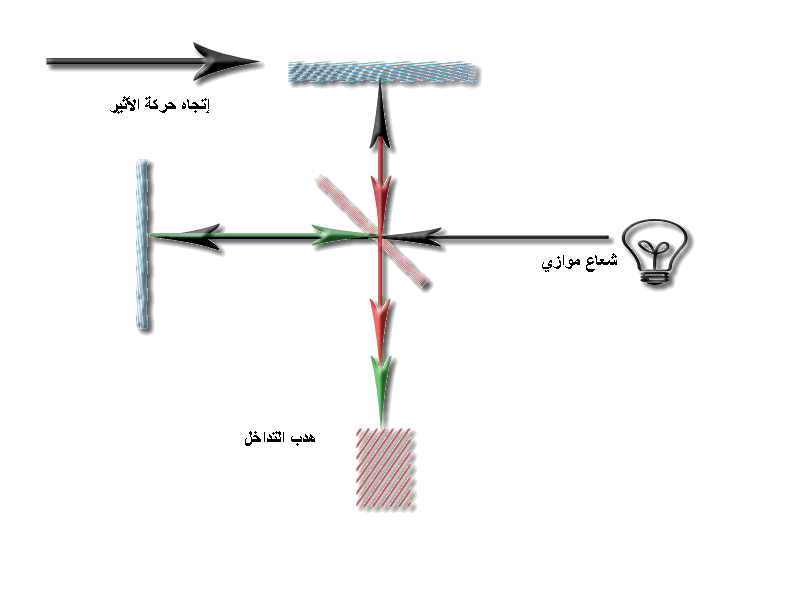
تجربة ميكلسون ومورلي

في عام 1886 بدأ ميكلسون ومورلي بتجاربهم عن انتشار الضوء وسرعته في الفضاء وكانوا يعتقدوا أنهم يستطيعون تحديد هذه السرعة عن طريق تعيين سرعة الأرض في مدارها حول الشمس بالنسبة للأثير والذي هو موجود في كل مكان مثل الهواء الذي يحيط بنا ولكن الأثير موجود في كل الكون وكانت نظرية ماكسويل الكهرومغناطيسية قد أثبتت أن الضوء ينتشر في الفضاء في صورة أمواج وكانت الأمواج تحتاج إلى وسط افترض انه الأثير الحامل للضوء فعوم ميكلسون اكتشاف الأثير بأن يقارن سرعة الضوء المتحرك في تجاه حركة الأرض بسرعة حزمة ضوئية تتحرك في اتجاه متعامد مع حركة الأرض وعندئذ لن يبرهن الفرق بين السرعتين على حركة الأرض فحسب بل انه يعطي فعليا سرعة الأرض في مدارها حول الشمس.

 وقد بنيت هذه التجربة على أساس نظري هو أنه إذا وجد الأثير فإن حركة الأرض فيه تولد تيارا أثيريا معاكسا لسرعة الأرض مثلما تولد المركبة تيارا هوائيا يجري معاكسا لحركتها فحين تقاس سرعة الضوء على الأرض فإن تأثرها بتيار هوائي يجري معاكسا لحركتها  وأثرها بتيار الأثير يتوقف على حركة الضوء هل هي موازاة لحركة الأرض أو معاكس لها أم هي متعامدة مع التيار.

وبدء العمل في هذه التجربة التي تمثل بسابحين أحرار في نهر احدهما يسبح مع النهر ذهابا وإيابا والأخر يبدأ من نفس النقطة الأولى ويسبح في عرض النهر ذهابا وإيابا ونفس المسافة التي يقطعها الأول يقطعها الثاني وفي نفس الوقت ويتضح من قانون جمع السرعات انه لا يمكن أن يعود السابحان في نفس الوقت لان السابح العرضي يصل أولا وهذا هو الأمر بالنسبة للضوء أيضا، وأعدا جهاز يستخدم في نقطة الأصل، وكان هذا الجهاز حساس إلى درجه عالية جدا ولكنه لم يسجل أي فرق في السرعتين وكانت هذه خيبة أمل لهما لأنه ظن انه اخفق في تجربته وأهمل ميكلسون هذه التجربة.

إلا أن الفيزيائيون عملوا على إجراء محاولة لتفسير هذه النتيجة ضمن إطار الفيزياء التقليدية وهذا التحليل رائع جدا ولكنه معقد واهم ماظهرت به هذه التحاليل هو أن الإليكترون الكروي يتفلطح نوعا ما عندما يتحرك في تجاه حركته بسبب خواص حركته الكهربائية وكلما أسرع كلما زاد تفلطحه ففكر لورتنز بأن المادة لكونها مؤلفه من إليكترونات تتفلطح إلى حد ما على طول خط حركتها، واستخدم هذا التفسير في تفسير تجربة ميكلسون ومورلي وأعلن أن الضوء الموازي لحركة الأرض نحو المرآة ذهابا وإيابا يتقلص في خط حركته يساوي بالتحديد الكميه الصحيحة اللازمة لإبطال التأخير الناتج عن تيار الأثير ويعرف هذا الأثر باسم فتزجيرالد- لورنتز في التقلص

3. تحويلات لورنتز

        وضع لورنتز معادلات التحويل على الصورة

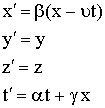                                                       (5)

حيث  ثلاث ثوابت يجب تعيينها ويجب أن تحقق هذه المعادلات معادلة الموجة الكورية في كلا النظامين. معادلة الموجة الضوئية الكورية كما ترى من النظام الأول هي

                                                       (6)

حيث c هي سرعة الضوء.

ومعادلة الموجة الكورية في النظام الثاني هي

                                                       (7)

بالتعويض في المعادلات (5) بقيم  في المعادلة (7) ومساواة معاملات كل كمية مع مثيلتها في المعادلة (6) نحصل على

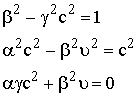                                                       (8)

وبحل هذه المعادلات تصبح معادلات لورنتز للتحويلات النسبية هي

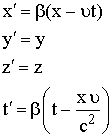                                                       (9)

حيث

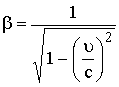                                                       (10)

ويمكننا إثبات أن سرعة الضوء ثابتة في كلا النظامين مما يحقق فروض النظرية النسبية.

4. تمدد الزمن وانكماش الطول

        تظهر تحويلات لورنتز مفاهيم جديدة تماما بالنسبة للطول والزمن. فإذا أخذنا قضيبا طوله L موازيا للمحور  ومتحركا معه بسرعة نسبية  بالنسبة لراصد في نظام آخر، وكانت إحداثيات النظام المتحرك هي  والثابت . نفرض أن طول القضيب بالنسبة للراصد في النظام الثابت هو L كما هو موضح في شكل (2).

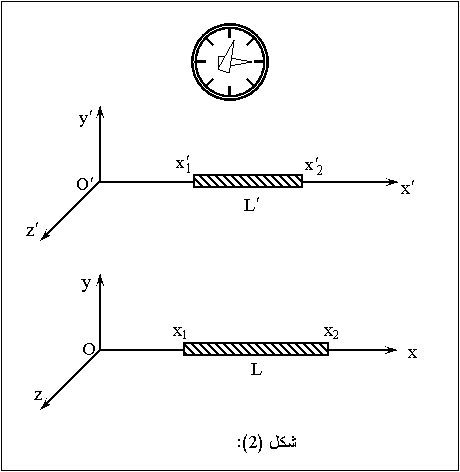
 من هذا الشكل نجد أن

    (11)

حيث x₁,x₂ هما إحداثيات نهايتي القضيب في النظام O’(x’,y’,z’)، طول القضيب نقسه هو L₂=x₂-x₁ في النظام O9x,y,z). باستخدام تحويلات لورنتز من المعادلات (9) في المعادلة (11) نجد أن

لكن

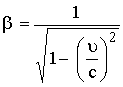
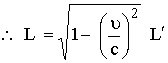    (12)

وحيث أن المقدار 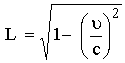 هو دائما أقل من الواحد الصحيح وأكبر من الصفر وذلك لأن  دائما فإن المقدار  أي أن الطول المقاس بالنسبة للراصد الساكن يكون أقل من ذلك بالنسبة للمتحرك وهذا هو ما يسمى بانكماش الطول.

        أما إذا اعتبرنا مسألة انكماش الزمن والفترات الزمنية بواسطة راصدين يتحركان بالنسبة لبعضهما فإننا نستخدم تحويلات لورنتز للزمن

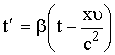    (13)

ونفرض ساعة مثبتة في نقطة ما في نظام متحرك  بالنسبة لنظام آخر O. نفرض أن الفترة الزمنية بين وقتين متتاليين كما يراها الراصد في النظام الثابت O هي . أما إذا كان الراصد متحركا مع النظام  المحتوى على الساعة فإنه يجد أن نفس الفترة الزمنية هي . وباستخدام المعادلة (13) نجد أن

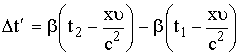
    (14)

ونظرا لأن  أكبر من الواحد الصحيح دائما فإن المقدار  أي أن الزمن يكون أكبر إذا قيس بواسطة راصد ساكن بالنسبة للساعة أي أن الساعة المتحركة تكون متأخرة كما تبدو لراصد ساكن بمعنى أن الزمن يتحدد بالنسبة إليه.

        وتظهر أهمية التمدد الزمني في عمليات انبعاث الإشعاع والتفتت النووي وتفاعلات الجسيمات الأولية وذلك لأن سرعاتها تكون كبيرة جدا وقريبة من سرعة الضوء مما يجعل التغير في قيمة  كبيرا.

مـثال(1): العمر الزمني لجسيم نووي قبل أن يتحول إلى صورة أخرى هو  ثانية وذلك حين يكون ساكنا في المعمل. ما عمر هذا الجسيم إذا أطلق بسرعة تساوى  من سرعة الضوء؟

الحـــل:  في هذه الحالة فإن  أي أن

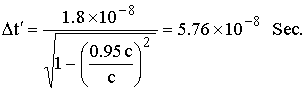
أي أن العمر الزمني للجسيم المتحرك يصبح حوالي ثلاثة أمثال عمره الزمني وهو ساكن.

مـثال (2): ما هي سرعة الطائرة والتي تدور الساعة الموجودة بها أبطأ بثانية لكل ساعة بالنسبة لساعة أخرى على سطح الأرض؟

الحــل:  بوضع                           ،

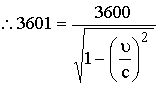
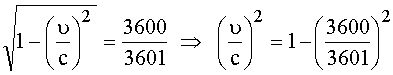
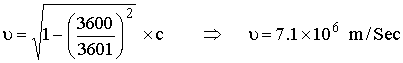
مـثال (3): إذا كان متوسط العمر للميزون () والذي يتحرك بسرعة  هو  احسب متوسط العمر له في النظام الساكن؟

الحــل:    ،

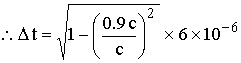
مـثال (4): تتحرك طائرة بالنسبة للأرض بسرعة  والطول الفعلي لها  ما هو مقدار النقص في الطول والذي يبدو أن الطائرة تنقصه بالنسبة لمشاهد على سطح الأرض؟

الحــل:  ، ،

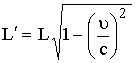
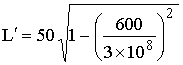
5. تغير الكتلة مع السرعة

        من أهم نتائج النظرية النسبية هو تأثير السرعة على كتلة الجسم المتحرك. فمن المعروف من الميكانيكا النيوتونية أن سرعة أي جسم كتلته m تتزايد بدون حدود إذا ما عجل بواسطة قوة F طالما استمر تأثير القوة عليه وفقا للمعادلة

                                                            (15)

حيث  هي سرعته عند أي لحظة زمنية t، a هي العجلة التي يكتسبها الجسم، . واضح أن السرعة  تزداد إلى ما لانهاية بعد زمن لا نهائي وهذه النتيجة غير صحيحة إذا اعتبرنا الفرض الأساسي للنظرية النسبية بأن هناك حد أقصى للسرعات هو سرعة الضوء. وللتغلب على هذه المشكلة يجب اعتبار أن كتلة الجسم تزداد بسرعة وفقا للمعادلة

                                                                                      (16)

حيث  هي كتلة السكون، m هي كتلته عندما يتحرك بسرعة  أي أن كتلة الجسم تصبح

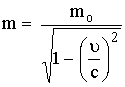                                                                        (17)

ويلاحظ أنه كلما اقتربت سرعة الجسم  من سرعته الضوء تزداد كتلته زيادة كبيرة وتقترب قيمتها من ما لانهاية إذا كانت  قريبة جدا من c. وهذه الكتلة الكبيرة تحتاج إلى قوة كبيرة لتعجيلها والقوة الكبيرة تلك غير متوفرة في الطبيعة.

6. كمية الحركة وطاقة الحركة لجسيم نسبوى

        كمية الحركة النسبوية للجسيم المتحرك بسرعة  تصبح

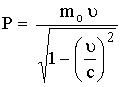                                                                     (18)

ولتعيين طاقة الحركة النسبوية للجسم نحسب الشغل المبذول W لزيادة سرعته من صفر إلي . عندما تؤثر قوة F على الجسم وأزاحته مسافة  في اتجاهها فإن

حيث

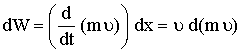
وبالتعويض عن الكتلة m من المعادلة (14) وإجراء التكامل نحصل على طاقة الحركة النسبوية للجسم KE

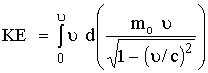
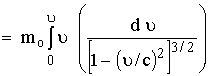
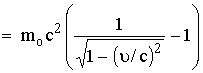
                                                                    (19)

أي أن طاقة الحركة لجسيم نسبوى تساوى فرق كتلتي الحركة والسكون مضروبة في مربع سرعة الضوء. وتسمى الكمية  بطاقة السكون،  بالطاقة الكلية للجسم. وفى هذه الحالة أيضا فإن طاقة الحركة تساوى الفرق بين الطاقة الكلية للجسم وطاقة السكون له. وتسمى المعادلة

                                                                    (20)

بمعادلة آينشتاين لتكافؤ الكتلة والطاقة.

مـثال (5): جسم كتلته خمسة كيلوجرام فما هي كتلته عندما يتحرك بسرعة مقدارها ؟

الحــل:    ،

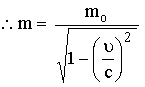
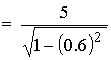
مـثال (6): كتلة جسيم يتحرك بسرعة  هي  أوجد كتله سكونه؟

الحــل:    ،

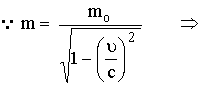
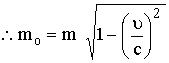
مـثال (7):إذا نجزأ جسم ساكن تلقائيا إلى جزأين متحركان في اتجاهين متضادين والجز آن لهما كتلة سكون  ،  على الترتيب وسرعتان مقداريهما  ،  حيث c سرعة الضوء. أوجد كتلة الجسم الأصلي ؟

الحــل:

 الطـاقــة الابتدائيــة  الطـاقــة النهائيــة

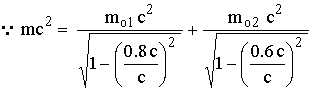
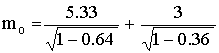
7. العلاقة بين كمية التحرك والطاقة لجسم نسبى

        بما أن كمية التحرك محفوظة فإنه من المفيد في غالب الأحيان التعبير عن طاقة جسم ما بدلالة كمية تحركه بدلا من سرعته كالآتي:-

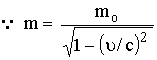
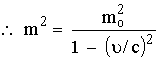
بضرب كلا من الطرفين في  نحصل على

وباستعمال النتائج

,     ,    

                                                                    (21)

8. وحدات الطاقة وكمية التحرك

        يعرف الإلكترون فولت (eV) بطاقة جسيم شحنته تساوى شحنة إلكترون واحد بعد تحركه خلال فرق جهد مقداره فولت واحد.

                                                                   (22)

والوحدات القياسية لكمية التحرك هي  إلا انه في الحسابات النسبية كثيرا ما تستعمل وحدات  لكمية التحرك وتنشأ هذه الوحدات من التعبير الخاص بالطاقة وكمية التحرك

مـثال (8): أحسب كمية تحرك الإلكترون والذي طاقة حركته 1 مليون إلكترون فولت. الحــل:

الطاقة الكلية   طاقة الحركة  طاقة السكون

  **  **  **  **  **  **  **  **  **  **  **  **  **  **  **  **  **

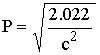
مـثال(9): عجل إلكترون إلى من السكون إلى سرعة مقدارها  احسب التغير في طاقته

الحــل:

وعند سرعة

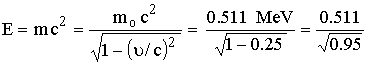
مـثال(10): أحسب طاقة الحركة لإلكترون كمية تحركه

الحــل:

  **  **  **  **  **  **  **  **  **  **  **  **  **  **  **  **  **

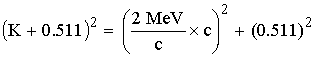
مـثال(11) أحسب سرعة إلكترون طاقة حركته

الحــل:

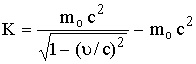
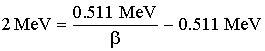
مـثال(12)

a) أحسب كتلة وسرعة إلكترون إذا علمت أن طاقته الحركية تساوى

b) ما هي الطاقة مقدرة بالإلكترون فولت اللازمة كي ينتقل إلكترون من السكون إلى سرعة مقدارها تسعة أعشار سرعة الضوء.

الحــل:

                                                                          (1)

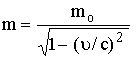                                                                           (2)

من المعادلة (1)                                               

كتلة الإلكترون                                            

سرعة الضوء                                                

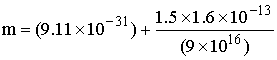
أي أن الكتلة أثناء الحركة حوالي أربع مرات الكتلة السكونية للإلكترون.

أما سرعة الإلكترون فنجدها من العلاقة (2)

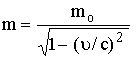
بتربيع الطرفين

**  **  **  **  **  **  **  **

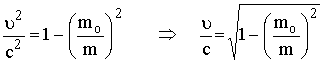
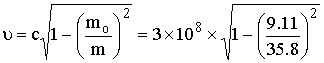
(b) نحسب الطاقة اللازمة لنقل الإلكترون من السكون إلى سرعة

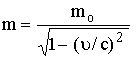
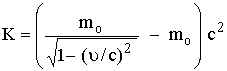
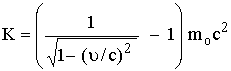
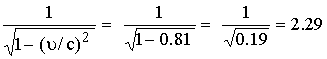
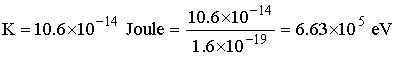
مـثال(13): يصدر عن نظير الكوبالت 60 لدى تفككه فوتونات من أشعة جاما وجسيم بيتا (إلكترون) طاقتة الحركية  فما هي سرعة جسيم بيتا المقذوف؟

الحــل:

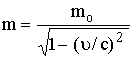
بتربيع الطرفين

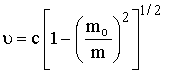
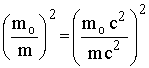
للإلكترون                                                

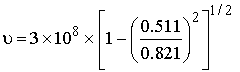
9. الأجسام التي ليس لها كتلة Mass less particles

هل يوجد جسيم ليس له كتلة؟ في الميكانيكا الكلاسيكية فإن الجسيم لابد أن يكون له كمية تحرك وطاقة، ولكن في النظرية النسبية هذه المعطيات لا تتحقق

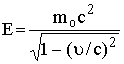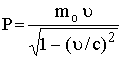  ,                                               (23)

(I) When and   

                                                                                   (24)

ولذلك فإن الجسيم الذي ليس له كتلة وسرعته أقل من سرعة الضوء ليس له طاقه ولا كمية حركة.

(II) When  and  

                                                                                   (25)

ويعن ذلك أن  ممكن أن يأخذا أي قيم.

إذن يشترط للجسم الذي ليس له كتلة أن تكون سرعته تساوى سرعة الضوء. وهذا هو الشرط الأول.

والشرط الثاني يمكن استنتاجه كالآتي:-

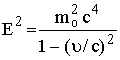                                                                            (26)

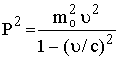
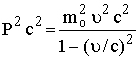                                                                        (27)

بطرح (2) من (1)

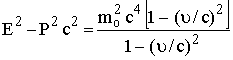
                                                                    (28)

وطبقا لهذه المعادلة لو وجد جسم كتلة سكونه  فإن العلاقة بين الطاقة وكمية الحركة تكون

                                                                                          (29)

وهذا هو الشرط الثاني للجسيمات التي ليس لها كتلة سكون.

10. تأثير دوبلر في النظرية النسبية The relativistic Doppler effect  

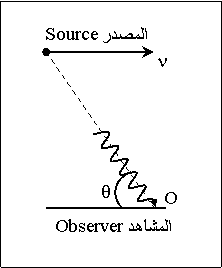
نفرض أن مصدرا يرسل أشعة كهرومغناطيسية بتردد قدره  بالنسبة لمشاهد في حالة السكون للمصدر. نفرض أن نفس المصدر في حالة حركة بالنسبة لمشاهد آخر والذي يقيس تردد الموجات الصادرة من المصدر . ويعطى التردد  والذي يسجله مشاهد عند  O بمعادلة دوبلر

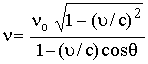(30)

ويكون عندنا الحالات الآتية:-

1. لو كان المصدر والمشاهد يتحركان تجاه بعضهما

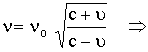
(30)

2. لو كان المصدر والمشاهد يتحركان بعيدا عن بعضيهما

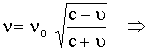
(31)

3. لو كان الإشعاع مستعرض لاتجاه الحركة

(32)

مسائل على الباب الأول

1. أثبت أن سرعة جسيم نسبوى  تحدد بالمعادلة

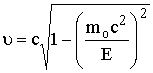
حيث E هي طاقته الكلية

2. زيدت سرعة إلكترون من  إلى  أوجد نسبة الزيادة في كتلته.

3. أوجد سرعة الجسيم النسبوى الذي كتلته تساوى ضعف كتلته سكونه وأوجد كمية حركته.

4. طول سفينة فضاء  ماذا يجب أن تكون سرعتها بالنسبة للأرض حتى يراها راصد أرضى بطول

5. يحتاج حدث معين إلي زمن قدره  لكي يحدث داخل ذرة فإذا تحركت الذرة بسرعة  فما هو الزمن الذي يقيسه راصد في المعمل لذلك الحدث.

6. شوكة رنانة ترددها  على الأرض. ماذا يكون ترددها داخل سفينة فضاء تسير بسرعة تساوى  ؟

7. في جهاز تعجيل البروتونات أمكن إعطاء البروتونات طاقة حركية مقدارها  ماذا يكون اختلاف سرعة البروتون عن سرعة الضوء؟ وماذا تكون كمية حركته؟

  **  **  **  **  **  **  **  **  **  **  **  **  **  **  **  **  **